Color of Light by Mixing Red and Green
Colour mixing and colour vision
| Additive primaries (red, green and blue) or subtractive primaries (cyan, magenta, yellow) can be mixed to make a very large, but not complete, set of colours. We show how this is done on an RGB monitor (additive) and using paints and filters (subtractive). The animation at right mixes the three additive primaries using your RGB monitor. This page supports the multimedia tutorials The Nature of Light and The Eye and Colour Vision.
|
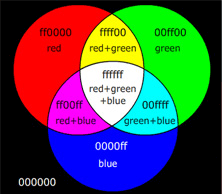
Colour mixing with additive and subtractive primariesThe animation below right shows additive mixing. The background is black, meaning that none of the pixels emit light, and our animation adds light over that black background. In the circle at top left, the red pixels vary from maximum to zero and back again. In the circle at top right, the green pixels vary. Where they overlap, we see red+green= yellow. In the bottom circle, the blue pixels vary, so we see, at left, blue+red=magenta and, at right, blue+green=cyan. In the centre, where all three circles overlap, we see red+green+blue=white. | ||||
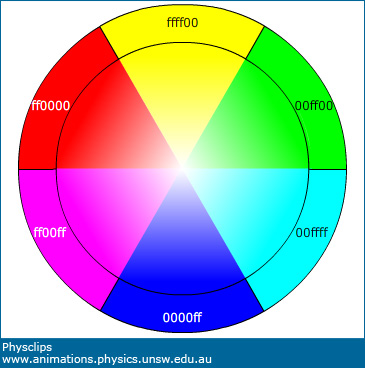
| The animation above left shows subtractive mixing. The background is white, meaning that the red, green and blue pixels all emit maximum light, and our animation subtracts from this white background. In the top circle, the red and green pixels are kept at maximum, while the blue pixels vary from zero to maximum and back again, so that the colour at the top varies from yellow (=red+green) to white (=red+green+blue) and back again. In the circle at right, the green and blue pixels are kept at maximum while the red pixels vary, so the colour at right goes from cyan (=green+blue) to white and back again. Where the yellow and cyan overlap, we see the subtractive mixture of yellow and cyan. In other words, we see white from which yellow has subtracted blue and cyan has subtracted red. This leaves green, i.e. the subtractive mix of yellow and cyan = white–blue–red = green. In the left circle, the red and blue pixels are kept at maximum, while the green pixels vary, so that the colour at left varies from magenta (red+blue) to white and back again. Where the yellow and magenta overlap, we see the subtractive mixture of yellow and magenta. In other words, we see white from which the yellow filter has subtracted blue and the magenta filter has subtracted green. This leaves red, i.e. the subtractive mix of yellow and magenta = white–blue–green = red. Where the magenta and cyan overlap, we see the subtractive mixture of magenta and cyan. In other words, we see white from which the magenta filter has subtracted green and the cyan filter has subtracted red. This leaves green, i.e. the subtractive mix of magenta and cyan = white–green–red = blue. Finally, where yellow, magenta and cyan overlap in the centre, we see the subtractive mixture of yellow, magenta and cyan. In other words, we see white from which the yellow filter has subtracted blue, the magenta filter has subtracted green and the cyan filter has subtracted red. This leaves nothing: the subtractive mix of yellow, magenta and cyan = white–blue–green–red = black. We return to Subtractive primaries and Subtractive colour mixing below. Additive colour mixing on RGB monitorsThe illustration at left shows several different colours. The numbers are six-digit hexadecimal representations of RGB colours. (Decimal goes from 0 to 9, hexadecimal extends this 9, a, b, c, d, e, f, to give 24 values per digit. The colour saturated red is usually written ff0000, but could also be written in decimal: 256;000;000.) The first two digits are the brightness of a red pixel, the next two that of the green, then that of blue. Consequently, 000000 is black, ff0000 is red, ffff00 is red+green, ffffff is white and so forth.
The right hand part of the picture is a close-up of a computer screen, which magnifies the red, yellow, white, magenta intersection. Looking at the right picture, at top left we see that only red components of each pixel are lit. At top right, both red and green are lit and, from a distance, these appear yellow (as in the picture at left). At bottom right, red, green and blue are all lit and the combination (centre of left picture) is a convincing white. If you have the room to move ten metres or so back from your screen, you'll see that the sections of the picture on the right really do become red, yellow, white and magenta (though the white is less bright than the surrounding white). If you'd like to examine this more closely, here are original close-up photographs (courtesy Noel Hanna) for the same illustration shown on a computer monitor and a smart-phone. If you download these files, you can zoom out or in (or walk backwards and forwards) to see the effect. | ||||
Why does three colour mixing work?
| The photoreceptors in your retina that respond to colour come in just three varieties, which we call 'red', 'green' and 'blue' according to the colour which produces maximal response. On the diagram at top right, the proportional response of the 'red', 'green' and 'blue' photoreceptors is shown as a function of wavelength. A three-colour representation of a spectrum is shown below the graph. Suppose that light from the yellow region of the spectrum, with a wavelength of say 580 nm, arrives at the retina. It lies between that of red (say 620 nm) and green (550 nm), so this light stimulates both red and green photoreceptors. This evokes a sensation that we are taught to call yellow. However, yellow that you see on the monitor is not light with wavelength near 580 nm. Instead, the monitor makes yellow colour using red light and green light from the same pixel. These two different wavelengths from the monitor are focussed onto a small area on your fovea, where it also stimulates red and green photoreceptors. So we perceive the effect as similar to light with wavelength 580 nm, even though no light of this wavelength is present. How does 'red+green' yellow compare with spectral yellow? We can't show you the difference, because you are (probably) looking at a RGB screen and it can only show you light with three wavelengths. No matter what we do, we can't get it to produce 580 nm! Nevertheless, most of us will admit that it is a passable yellow (for human eyes, at least).Many species of insects and birds have four-colour vision, often with sensitivity to near ultraviolet light. Some flowers have petals that are patterned in the UV but which appear homogeneous to us. | 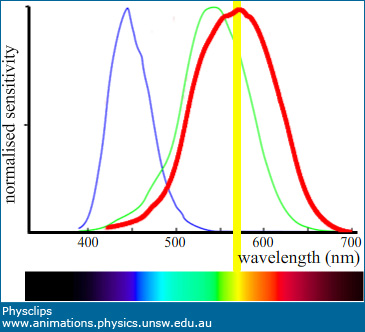 Human three colour vision |
Additive colour mixing by projectionLet's look at other ways of adding colours. In this movie, we use three slide projectors, with red, green and blue filters. We vary the intensity in each successively. Depending on your screen, your eyes and your vocabulary, you'll probably see that, once again,
Of course, we are showing you the movie on a RGB monitor, so we are still using combinations of RGB pixels. |
Newton's colour wheelOne way of combining colours, without a computer monitor, is to illuminate a rotating wheel whose sectors are painted in different colours. The eye integrates light over a few tens of milliseconds, so in that sense it adds the colours that are successively presented at a given point on the retina. We demonstrate that here, using a drill to rotate the wheel. Here, the combination of colours cannot be brighter than the average of all of the colours so, on the monitor, it appears grey rather than white. Of course, if we compare grey in bright light and white in dim light we may not see a difference. |
More on subtractive primaries
We all remember our first set of paints: red paint plus green paint do not make yellow! Yes, there's a big difference: with paints we are not adding light, but subtracting it. White paper reflects all colours; when we add coloured paint to it, that paint allows some colours to pass through, but absorbs (subtracts) others. Just as most colours can be made by mixing light with proportions of the three additive primaries, we can also produce most colours by starting with white light and subtracting different proportions of three subtractive primaries:
The subtractive primaries are these:
We hope you've noticed that the subtractive primaries are the complementary colours of the additive primaries. In the diagrams below, we represent white light as made of red + green + blue, because it stimulates our red, green and blue photoreceptors. In practice, you are probably reading this on an RGB monitor, then the white really is made from an RGB pixel combination.
| Subtractive mixing: e.g. paint on a page filters the incident (white) light. |
We can expand those in still diagrams: white light is represented in the top row: it then passes through each of the subtractive primary filters to give the colour in the bottom row:
Magenta filter
Cyan filter
Yellow filter
Subtractive colour mixing
What do we get if we add magenta + cyan paint? We can extend these diagrams to answer that question.| Mixing subtractive primaries: each filter removes some of the incident light. |
Or, if you prefer tables to the animation above:
Yellow filter + cyan filter
Yellow filter + magenta filter
Magenta filter + cyan filter
Combining three subtractive filters
| Subtractive mixing with three filters |
Again, we can show this in a still diagram: Cyan filter + yellow filter + magenta filter
However, this is not really subtractive mixing: if you are reading this on a monitor, then all the colours and white are made from different proportions of red, green and blue. If you want to see real subtractive mixing, you could print it out. Your printer will start with white paper and then print a mixture of cyan, yellow, magenta and black pigments. There are two reasons for the black pigment in printers: first, a mixture of CYM can, with adjustment, give reasonable dark grey. Also, black pigment is usually cheaper than a CYM mixture.
Complementary colours |
| As we've mentioned above, the subtractive primaries are the complementary colours of the additive primaries. See the support page Complementary Colours for more detail and for demonstrations of how complementary colours may be evoked by retinal fatigue. |
3, 4, 5, 6, 7 or many colours?
Three additive and three subtractive primaries? 6 in total? Then what happened to the ROYGBIV rainbow that we learned at school? While the three primaries are (for humans, at least) a logical set, divisions of the spectrum are arbitrary. As for much else, it appears that we have Newton to thank for the 7-coloured rainbow. Fisher (2015) writes "The medieval rainbow had just five colours: red, yellow, green, blue and violet. Newton added two more � orange and indigo � so that the colours would be �divided after the manner of a Musical Chord� (I. Newton in Opticks 4th edn, 127 (William Innys), 1730)".
In several of the figures above, the (varying) colour is indicated by a hexadecimal number, such as ff0000. The first two digits give the hexadecimal proportion of red, the next to green, the final two blue (pause the animations and check that 00ff00 is green, 0000ff is blue, and ffff00 is yellow). Hexadecimal means that each digit counts successively 1,2,3,4,5,6,7,8,9,a,b,c,d,e,f,0. So 10 in hexadecimal is 16 in decimal, and 100 in hexadecimal is 162 = 256. So this numbering system can label 2563 = 16,777,216 colours, which is probably enough even for an interior decorator. Many graphics packages allow you to specify colours by with six digit hexadecimals (or sometimes six decimal digits), so you can experiment with these. (Incidentally, Newton's choice of 'orange' as a name was a good one. It is now echoed by such colours as apricot, peach, avocado etc.)
The following link takes you back to the multimedia tutorials The Nature of Light and The Eye and Colour Vision.
Color of Light by Mixing Red and Green
Source: https://www.animations.physics.unsw.edu.au/jw/light/colour-mixing.htm

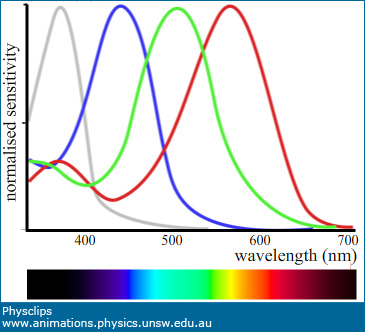 A four colour vision system
A four colour vision system